Modèle mathématique
Utiliser cette image
Puis-je réutiliser cette image sans autorisation? Oui
Les images sur le portail de la collection d’Ingenium ont la licence Creative Commons suivante :
Copyright Ingenium / CC BY-NC-ND (Attribution-NonCommercial 4.0 International (CC BY-NC 4.0)
ATTRIBUER CETTE IMAGE
Ingenium,
2016.0088.007
Permalien:
Ingenium diffuse cette image sous le cadre de licence Creative Commons et encourage son téléchargement et sa réutilisation à des fins non commerciales. Veuillez mentionner Ingenium et citer le numéro de l’artefact.
TÉLÉCHARGER L’IMAGEACHETER CETTE IMAGE
Cette image peut être utilisée gratuitement pour des fins non commerciales.
Pour un usage commercial, veuillez consulter nos frais de reproduction et communiquer avec nous pour acheter l’image.
- TYPE D’OBJET
- S/O
- DATE
- 1930
- NUMÉRO DE L’ARTEFACT
- 2016.0088.007
- FABRICANT
- Flather, H.T.
- MODÈLE
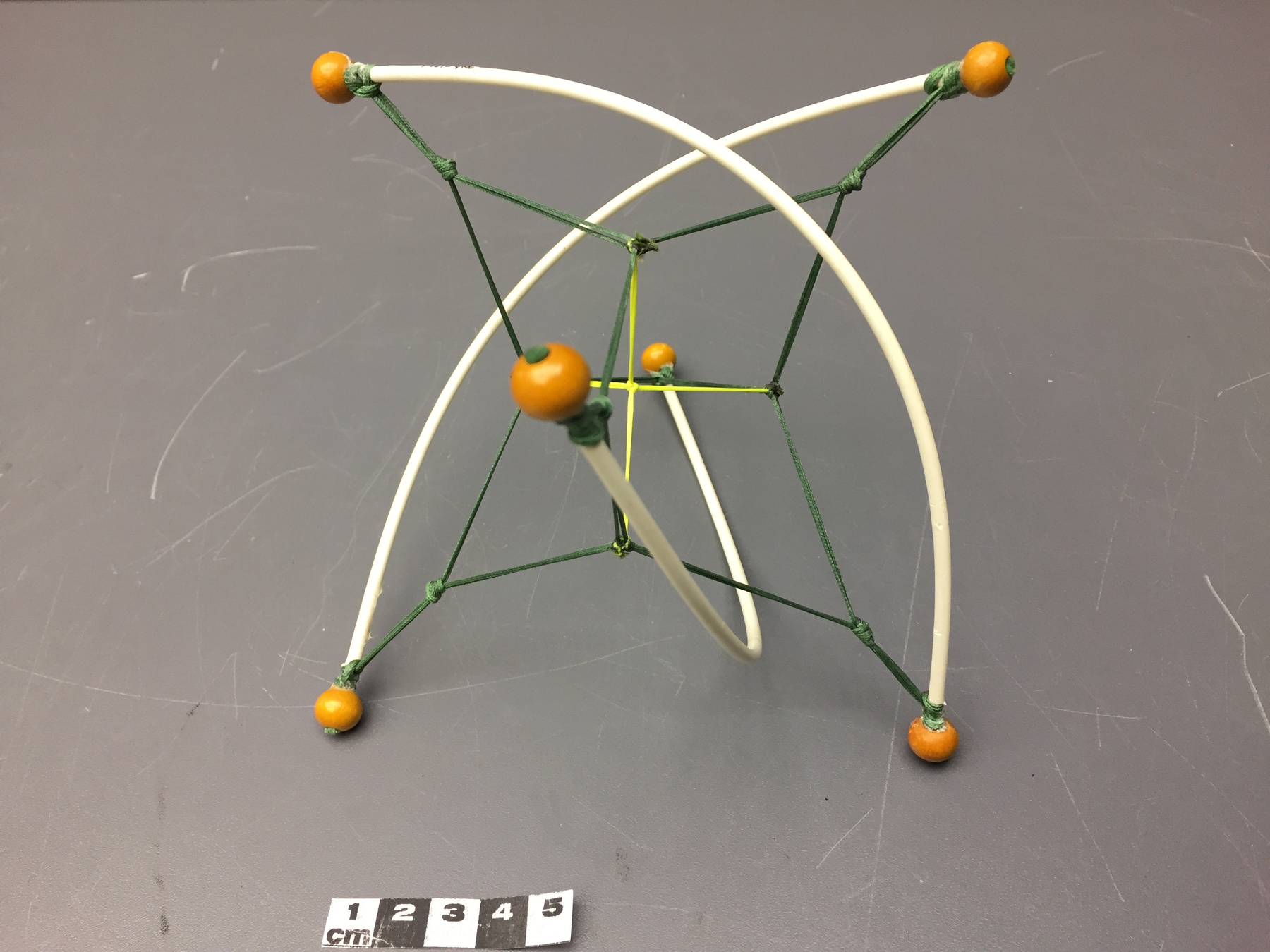
- Icosahedron
- EMPLACEMENT
- England
Plus d’information
Renseignements généraux
- Nº de série
- S/O
- Nº de partie
- 7
- Nombre total de parties
- 12
- Ou
- S/O
- Brevets
- S/O
- Description générale
- Card stock
Dimensions
Remarque : Cette information reflète la taille générale pour l’entreposage et ne représente pas nécessairement les véritables dimensions de l’objet.
- Longueur
- 4,2 cm
- Largeur
- 4,7 cm
- Hauteur
- 1,8 cm
- Épaisseur
- S/O
- Poids
- S/O
- Diamètre
- S/O
- Volume
- S/O
Lexique
- Groupe
- Mathématiques
- Catégorie
- Maquettes
- Sous-catégorie
- S/O
Fabricant
- Ou
- Flather
- Pays
- England
- État/province
- Inconnu
- Ville
- Inconnu
Contexte
- Pays
- Inconnu
- État/province
- Inconnu
- Période
- C. 1930 - 2003
- Canada
-
Taken from acquisition proposal: "This collection of models comes from the personal collection of H.S.M. Coxeter (1907-2003), one of Canada's more renowned mathematicians. At the age of sixteen, Coxeter won a prize for an essay on "dimensional analogy." This essay attracted the attention of Bertrand Russell, a friend of his father, and the young prodigy was promptly put on course for mathematics at Cambridge. He earned his B.A. there in 1929, and his Ph.D. in 1931 working under H.F. Baker. In 1936 Coxeter traveled across the Atlantic to join the Mathematics Department at Toronto, where he remained until his death in 2003. During his long career, Coxeter has made significant contributions to non-Euclidean geometry and to the theory of polytopes (the stretching of geometric shapes into higher dimensions). Many geometers today use what are called Coxeter groups, or groups that are generated by reflections. Coxeter refers to them simply as the "algebraic expression of how many images of an object may be seen in a Kaleidoscope." Coxeter's work on group presentations, which was published in 1957 under the title Generators and Relations for Discrete Groups, attracted the attention of non-geometers as well. He became a friend of the Dutch graphic artist, M.C. Escher, and the American architect, Buckminster Fuller. It is a great irony that as geometry struggled to keep its stature in mathematics departments throughout Coxeter's lifetime, at times, particularly in the sixties, it enjoyed a popular form of expression outside of academia in painting, sculpture, architecture and furniture. One need only look at Montreal's Expo '67 to see the pervasive influence of geometry on our culture in that period. Fine examples included US Pavilion - the 20 story geodesic dome of Buckminster Fuller, the "space frame" architecture of the Netherland's pavilion, the Explorer and Producer buildings, the mirrored reflections of the Kleidoscope pavilion, as well as the geometric trash bins.". The Models: "Coxeter's collection represents the diverse people involved in making models: fellow mathematicians, artists, amateurs, former students and colleagues inspired and influenced by his multifaceted contributions to geometry. This is certainly the case of the 24 icosahedra made by H.T. Flather, who made the complete set in the late 1930s (the others are preserved in the mathematics library of Cambridge University). Flather shipped the 24 models to Coxeter prior to Second World War for safekeeping. Coxeter was told to keep them following the war. John Robinson built Firmament derived from a challenging problem that Coxeter had posed to him related to five spheres in mutual contact where the points of contact form interesting mathematical relations in space. The models seem relatively simple in form, but for Coxeter even the most basic shapes represented difficult boundaries between higher mathematics and the world of everyday experience. This is a tension that Coxeter seemed to thrive on; he clearly saw things in the models that most others would find impossible to imagine, and this must be one of the main reasons that he has kept and displayed them. On the subject of analogous figures in four or more dimensions, he once wrote: "we can never fully comprehend them by direct observation. In attempting to do so, however, we seem to peep through a chink in the wall of our physical limitations, into a new world of dazzling beauty. Such an escape from the turbulence of ordinary life will perhaps help us to keep sane." As historian David Roberts has written: "He [Coxeter] was as charmed as anyone by individual models, more charmed indeed than most highbrow mathematicians, but for him models were only the beginning; for Coxeter there could even come a point in an investigation beyond which models served more to obscure than to clarify." Coxeter certainly relied on the models as an aid for transmitting his ideas and as an entry into more abstract realms of mathematics. One can clearly see by the size and diversity of the collection, and by the fact that they were well-preserved and displayed, that Coxeter found them to be inspirational objects and springboards for an active mathematical imagination. They also represent a kind of three-dimensional correspondence with amateurs, students and artists reflecting the deep impact Coxeter had on twentieth-century geometry.". - Fonction
-
Used as a visual aid for teaching mathematics. - Technique
-
Inconnu - Notes sur la région
-
Inconnu
Détails
- Marques
- None apparent.
- Manque
- Appears complete
- Fini
- Painted greyish-white card stock formed in a mathematical shape.
- Décoration
- S/O
FAIRE RÉFÉRENCE À CET OBJET
Si vous souhaitez publier de l’information sur cet objet de collection, veuillez indiquer ce qui suit :
Flather, H.T., Modèle mathématique, vers 1930, Numéro de l'artefact 2016.0088, Ingenium - Musées des sciences et de l'innovation du Canada, http://collections.ingeniumcanada.org/fr/item/2016.0088.007/
RÉTROACTION
Envoyer une question ou un commentaire sur cet artefact.
Plus comme ceci